Cara Menghitung Peluang, Rumus, Konsep & Latihan Soalnya

Yuk, belajar mengenai konsep dasar, rumus, dan cara menghitung teori peluang suatu kejadian dalam Matematika.

—

Tiap mau keluar rumah, pernah nggak sih kamu cek prakiraan cuaca?

Kalo aku pernah tuh, ngeceknya sampai berkali-kali lagi. Takut di tengah jalan tiba-tiba kehujanan dan basah kuyup. 

Akses prakiraan cuaca juga udah simple banget ya, karena di setiap handphone udah ada aplikasinya sendiri.

Eits, tapi kamu tau nggak? Di kondisi tadi, tanpa sadar sebenarnya kita lagi menerapkan prinsip peluang loh. Nah, konsep peluang ini masuk ke pelajaran matematika dari jenjang SMP sampai SMA. Bahkan, teori peluang cukup sering keluar di ujian masuk perguruan tinggi atau UTBK. Kebayang dong begitu pentingnya konsep peluang ini buat dipelajari.

Yaudah, yuk langsung aja kita kepoin konsep teori peluang ini!

Pengertian Peluang

Apa sih maksud dari peluang dalam matematika? Sederhananya, peluang adalah kemungkinan terjadinya suatu kejadian.  Misalnya, kelas 10 IPA 2 memiliki 30 siswa. Dari jumlah tersebut, akan dipilih 10 orang sebagai panitia pentas seni. Ternyata, kamu terpilih diantara 10 orang itu.

Nah, kejadian terpilihnya kamu disebut sebagai peluang.

Oh iya, di awal tadi kan kamu sudah tau kalau prakiraan cuaca merupakan salah satu contoh penerapan prinsip peluang. Tapi nggak cuma itu aja ya, karena penerapan peluang tuh banyak banget di kehidupan sehari-hari. Contohnya, untuk asuransi, modal kamu belajar investasi, dan masih banyak lagi.

Di dalam teori peluang, terdapat 4 hal yang penting untuk kamu ingat, yaitu percobaan, ruang sampel, titik sampel, dan kejadian.

Baca juga: Pemahaman Konsep & Latihan Soal Transformasi Geometri

Percobaan Peluang

Apa itu percobaan peluang? Artinya kegiatan atau tindakan yang tujuannya untuk memperoleh hasil tertentu. Misalnya, pelemparan uang koin, pelemparan dadu, pengambilan kartu, pengambilan bola secara acak, sampai mencari pasangan tempat duduk.  

Ruang Sampel Peluang

Nah, hasil dari percobaan di atas disebutnya ruang sampel. Jadi, bisa dibilang ruang sampel adalah himpunan semua hasil yang mungkin dari suatu percobaan. Ruang sampel itu simbolnya S ya. 

Contoh ruang sampel, gini. Misalnya kita melakukan percobaan pelemparan 1 uang koin. Kemungkinan yang muncul kan bisa angka dan bisa juga gambar. Jadi, ruang sampelnya adalah sisi angka dan sisi gambar. 

Kalau ditulis, rumus himpunan ruang sampel adalah S= {Sisi angka, Sisi gambar}.

Titik Sampel Peluang

Setiap anggota dari ruang sampel, itu dinamakan titik sampel. Atau gampangnya kamu liat aja tuh anggota dari himpunannya.

Kalo dari percobaan di atas, jadi titik sampelnya ada sisi angka dan gambar. 

Oh iya, kalau di soal biasanya ditanya jumlah titik sampel. Nah, kamu bisa tulisnya gini, n(S)= 2.

Untuk kondisi yang lebih kompleks, kamu bisa nentuin titik sampel dengan berbagai cara. Bisa pakai diagram pohon, tabel dan aturan pencacahan.

Contoh:

Kita akan menentukan titik sampel dari percobaan pelemparan dua uang koin sekaligus.

1. Rumus Titik Sampel dengan Diagram Pohon

2. Rumus Titik Sampel dengan Tabel

Jadi, S={(A,A), (A,G), (G,A), (G,G)}.

Nah, kalo ditanya berapa banyak titik sampelnya, yaudah kita bisa tulis:

 n(s) = 2 x 2 = 4

Kamu pasti udah nungguin kan cara ketiga, yaitu menentukan titik sampel dengan aturan pencacahan.

3. Aturan Pencacahan

Untuk yang menentukan titik sampel dengan aturan pencacahan, kita bisa menggunakan rumus-rumus dari aturan permutasi dan aturan kombinasi.

Masih inget nggak perbedaan dari aturan permutasi dan kombinasi?

Aturan permutasi memperhatikan urutan atau susunan. Sedangkan kombinasi diambil secara acak, random, atau tanpa memperhatikan urutan.

Baca juga: Latihan Soal dan Pembahasan Penalaran Matematika UTBK SNBT 2023

Jenis Kejadian Peluang dan Contohnya

Maksud dari kejadian di materi peluang ini adalah himpunan bagian dari ruang sampel. Biasanya dituliskan dengan huruf kapital, seperti A, B, dll.

Ada 2 jenis kejadian peluang dalam matematika, yaitu Kejadian Tunggal dan Kejadian Majemuk. Kejadian Tunggal hanya terdiri dari 1 kejadian, sedangkan Kejadian Majemuk memiliki dua atau lebih kejadian secara bersamaan.

Supaya kamu lebih paham dan tau banget perbedaannya, kita latihan soal ya!

SOAL 1

Pada percobaan pelemparan sebuah dadu bermata 6.

Dimana, A= Kejadian muncul mata dadu kurang dari 3. Maka himpunan kejadiannya adalah…

Penyelesaian:

Dari soal di atas kan, diketahui hanya melempar satu dadu. Kita bisa menyimpulkan bahwa soal 1 ini adalah kejadian tunggal.

Berarti S={1,2,3,4,5,6}

Karena kejadian yang muncul mata dadu kurang dari 3, maka, A={1,2}.

SOAL 2

Pada percobaan pelemparan dadu bermata 6. 

Dimana, D: Kejadian muncul mata dadu kurang dari 3 atau mata dadu ganjil.

Penyelesaian:

Soal ini udah pasti termasuk kejadian majemuk ya, guys. Triknya kamu liat aja di kalimatnya ada kata atau.

A= Kejadian muncul mata dadu kurang dari 3 

B= Kejadian mata dadu ganjil

Kita bisa tahu ya, untuk A={1,2} dan B={1,3,5}

Di materi peluang ini kata “atau” diartikan dengan gabungkan kejadian A dan B.

Yaudah kita gabungin aja, jadi D={1,2,3,5}

Ingat! Kalo disoal adanya kata dan maka kamu harus mencari irisan kejadian 1 dan lainnya.

Rumus Peluang Teoritis dan Peluang Empiris

Wah, udah lengkap banget tuh konsep awal peluang di atas. 

“Eh, tapi dari tadi kita bahas keempat bagian dari peluangnya, nah gimana tuh kalo di soal nanya tentang peluang dari suatu kejadian?”

Peluang sendiri itu ada peluang teoritis dan peluang empiris. 

“Aduh, bedanya apa tuh?”

Eits, tenang ini nggak ribet kok! 

1. Rumus Peluang Teoritis

Ada satu hal yang wajib banget kamu inget. Jadi kisaran nilai peluang itu dari 0 sampai 1. Kalo hasil hitung kamu adalah nol, berarti kejadiannya mustahil dan kalo hasilnya 1 biasanya menunjukkan kejadian tertentu. 

Makanya guys, kalo hasil perhitungan peluang kamu lebih dari 1 atau kurang dari 0, berarti kamu salah ngitung tuh wkwkwk.

2. Rumus Peluang Komplemen

Di peluang ini kamu akan ketemu dengan simbol kaya gini 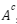, yang dibaca peluang komplemen. Ini basic sih, karena materi matematika juga sering ada simbol komplemen. Jadi artinya, peluang semua kejadian yang bukan A.

3. Rumus Peluang Empiris

Aku punya tips nih, supaya kamu lebih gampang untuk membedakan peluang empirik. Intinya, kalo dalam soal sudah ada data hasil percobaan lain atau kejadian sebelumnya maka itu adalah peluang empirik.

Mendingan kita langsung bahas soal aja yuk, supaya kamu makin tau letak perbedaan, cara menghitung, jenis-jenis peluang yang sudah dijelaskan tadi!

Contoh Latihan Soal dan Pembahasan Peluang

Soal 1

Terdapat sebuah kantong berisi 3 bola merah, 4 bola biru, dan 2 bola ungu. Kakak akan mengambil  3 bola sekaligus dari kantong ini. Maka peluang terambilnya ketiga bola biru adalah…

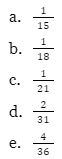
Pembahasan:

Soal ini termasuk dalam peluang teoritis, kita sudah tau rumus dari peluang teoritis adalah:

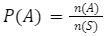
Jadi kita cari dulu n(A) dan n(S) nya, yuk!

Total bola yang ada dalam kantong adalah 3+4+2=9.

Dari soal diketahui kakak akan mengambil 3 bola dari 9 bola.

Kita bisa pakai rumus kombinasi ya, karena nggak memperhatikan susunan. 

Jadi banyak titik sampel atau [n(S)] :

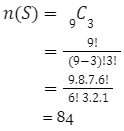
Udah dapet nih n(S)= 84

Sekarang kita cari n(A) atau kejadian terambil ketiganya bola biru. Btw, tetap pake rumus kombinasi ya!

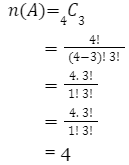
Maka peluang kejadian A :

Soal 2

Peluang hari ini hujan adalah 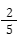 kali peluang hari ini tidak hujan. Peluang hari ini hujan adalah…

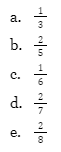
yuk kamu bisa coba sendiri dulu ya!

Pembahasan:

Kita misalkan A = kejadian hari ini hujan.

Dari soal diketahui Peluang hari ini hujan adalah 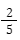kali peluang hari ini tidak hujan.

Berarti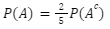

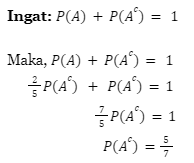
Nah, dari sini kita bisa tau nilai P(A) nya:

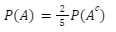
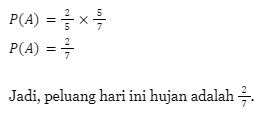
Soal 3

Pada pertandingan basket yang dilaksanakan di Indonesia sebanyak 18 kali, tim Indonesia menang 9 kali, seri 2, dan kalah 7 kali. Peluang Tim Indonesia akan menang adalah…

1. 0
2.  1/2
3. 2/5
4. 3/2
5. 3/5

Pembahasan:

Oke, kalo kita liat dari soal ini termasuk peluang empiris ya. Karena udah diketahui data hasil pertandingan sebelumnya.

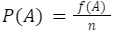
dimana f(A)=9 dan total pertandingan atau n=18. Maka:

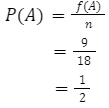
Jadi, peluang Tim Indonesia akan menang adalah ½ .

—

Masih ada yang belum kamu pahami? Yuk, belajar bersama STAR Master Teacher di Brain Academy! Rumus matematika yang sulit bakal dijelaskan dengan cara yang seru dan anti ngantuk. Pasti nilai kamu langsung 100, deh. Nggak percaya? Bisa coba kelas gratis dulu kok.

Artikel ini terakhir diperbarui tanggal 17 Januari 2023.